Fast Fourier Transform (FFT)

本單元介紹快速傅立葉轉換法 (Fast Fourier Transform, 簡稱 FFT). FFT 常被利用於計算兩多項式的相乘，即給定兩個 \( n \) 次多項式，求兩多項式的乘積。直覺上有個 \( \Theta(n^2) \) 的算法是將係數逐一相乘再相加，而 FFT 利用分治法提供時間為 \( \Theta(n \log n) \) 的算法。為了討論方便，我們有以下假設：

• 所有 \( n \) 皆為 \( 2 \) 的冪次方, 即存在正整數 \( k \) 使得 \( n = 2^k \).
• 多項式 \( A(x) \) 和 \( B(x) \) 為被乘式和乘式，次方為 \( n-1 \) 次。相乘結果為 \( 2n-2 \) 次多項式 \( C(x) \).

實作上，若 \( n-1 \) 次多項式的 \( n \) 不為 \( 2 \) 的冪次，我們會將多項式拓展至 \( m-1 \) 次，並在新增的次方係數補零，其中 \( m \) 為大於 \( n \) 且為 \( 2 \) 的冪次中最小的數。例如我們會將 $$ 5x^4+4x^3+3x^2+2x+1 $$ 拓展至 $$ 0x^7+0x^6+0x^5+5x^4+4x^3+3x^2+2x+1 $$

若 \( A(x) \) 和 \( B(x) \) 的次數不同，我們也會將兩多項式拓展至相同次數。

本文首先介紹兩種多項式的表示式，這兩種表示式之間的轉換就是 FFT, 其性質在本文扮演重要的角色。再來介紹 \( n \) 次單位根 (The principal nth root of unity) 和范德蒙矩陣 (Vandermonde matrix) 兩個數學工具。這兩個數學工具會在後面操作分治法時有很大的幫助。最後會將所有工具和計算方法合併，得到一個透過 FFT 在 \( \Theta(n \log n) \) 時間完成多項式相乘的演算法。

多項式表示式

較廣為人用的多項式表示法有以下兩種：

係數表示式 (Coefficient representation)

給定 \( n-1 \) 次多項式 \( A(x) = a_0 + a_1x + a_2x^2 + \cdots + a_{n-1}x^{n-1} \). 我們將係數取出形成一個向量 \( a = (a_0, a_1, \cdots, a_{n-1}) \). 該向量即為 \( A(x) \) 的係數表示式。係數表示式是兩者中最常被使用的，同時也是 \( A(x)\) 和 \( B(x) \) 兩多項式最一開始的表示式。

點值表示式 (Point-value representation)

給定實數平面上相異且不共 \( n-2 \) 次多項式的 \( n \) 個點。這 \( n \) 個點能唯一決定一個 \( n-1 \) 次多項式。若集合 \( S_A = \{(x_0, y_0), (x_1, y_1), \cdots, (x_{n-1}, y_{n-1})\} \) 中，每個元素皆滿足 \( y = A(x) \), 且任何 \( n-2 \) 次多項式都無法包含所有點，則我們稱 \( S_A \) 為 \( n-1 \) 次多項式 \( A(x) \) 的點值表示式。注意上述條件讓 \( S_A \) 可以不只有 \( n \) 個點但至少需要有 \( n \) 個點.

點值表示式的好處在於可以花 \( \Theta(n) \) 的時間計算多項式相乘。若以點值表示式給定 \( A(x), B(x) \) 兩個 \( n-1 \) 次多項式，只需要 \( \Theta(n) \) 的時間即可得到 \( C(x) \) 的點值表示式。

例如給定 \( S_A, S_B \) 兩基數為 \( 2n-1 \) 關於 \( n-1 \) 次多項式 \( A(x) \) 和 \( B(x) \)的點值表示式 $$ S_A = \{(x_0, A(x_0)), (x_1, A(x_1)), \cdots, (x_{2n-2}, A(x_{2n-2}))\} $$ $$ S_B = \{(x_0, B(x_0)), (x_1, B(x_1)), \cdots, (x_{2n-2}, B(x_{2n-2}))\} $$ 將兩集合擁有相同 \( x \) 座標的 \( y \) 值相乘，得到基數為 \( 2n-1 \) 的集合 \( S_C \) $$ S_C = \{(x_0, A(x_0) \cdot B(x_0)), (x_1, A(x_1) \cdot B(x_1)), \cdots, (x_{2n-2}, A(x_{2n-2}) \cdot B(x_{2n-2}))\} $$ 該集合就是 \( C(x) \) 的點值表示式。

回到起點，我們探究的是利用 FFT 將兩個以係數表示式呈現的多項式相乘，得到以係數表示式呈現的新多項式。目前我們所擁有的工具是在 \( \Theta(n) \) 的時間將兩個點值表示式相乘。如下圖，若可以掌握兩種多項式表示式間的轉換，多項式的乘法就完成了。

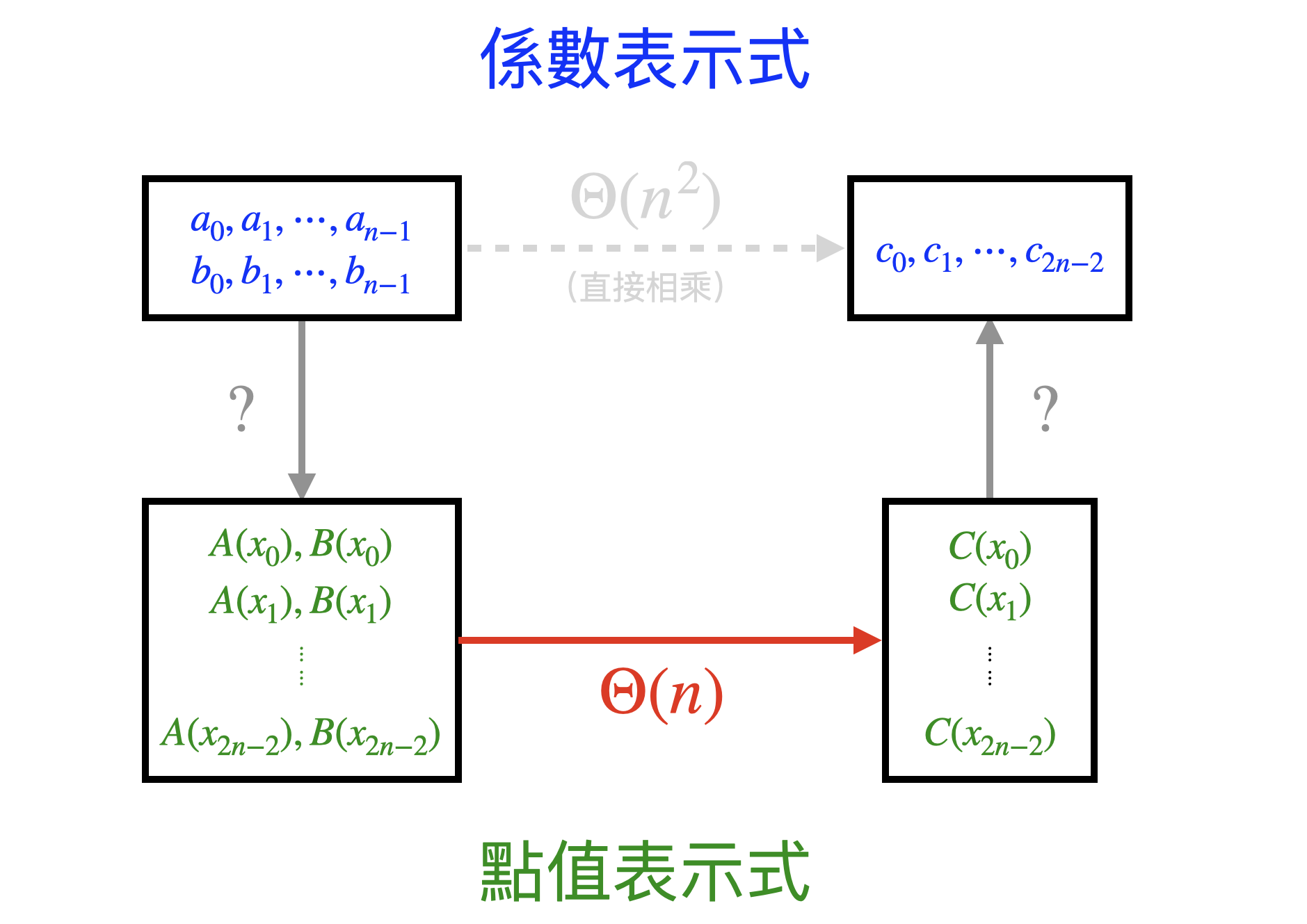
因此我們要知道兩表示式間如何轉換。

兩表示式間的轉換

已知 \( n-1 \) 次多項式 \( A(x) \Rightarrow \) 求 \( S_A \) (\( |S_A| = n \))

任選 \( n \) 個點 \( x_0, x_1, \cdots, x_{n-1} \) 並代入 \( A(x) \) 即得 \( S_A = \{(x_0, A(x_0)), (x_1, A(x_1)), \cdots, (x_{n-1}, A(x_{n-1}))\} \)

觀察得每個值 \( A(x_i) \) 都是向量 \( (a_0, a_1, \cdots, a_{n-1}) \) 和 \( (1, x_i, x^2_i, \cdots, x^{n-1}_i) \) 的內積。

因此我們可以把求值的過程表示成下列矩陣計算：

$$ \left( \begin{matrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \end{matrix} \right) \left( \begin{matrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{matrix} \right) = \left( \begin{matrix} A(x_0) \\ A(x_1) \\ A(x_2) \\ \vdots \\ A(x_{n-1}) \end{matrix} \right) $$

為了後面方便描述，我們稱左式中的方陣為 \( V_n \), 其中下標 \( n \) 為方陣大小。

已知 \( S_A ( |S_A| = n ) \Rightarrow \) 求 \( n-1 \) 次多項式 \( A(x) \)

使用類似的手法，現在要求的是向量 \( (a_0, a_1, \cdots, a_{n-1}) \). 故只需求得 \( V_n \) 的反矩陣後即可運算

$$ \left( \begin{matrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \end{matrix} \right)^{-1} \left( \begin{matrix} A(x_0) \\ A(x_1) \\ A(x_2) \\ \vdots \\ A(x_{n-1}) \end{matrix} \right) = \left( \begin{matrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{matrix} \right) $$

到這裡，一個很大的瓶頸是：方陣大小如此大的反矩陣要如何計算？一般而言，任意給定相異 \( n \) 數 \( x_0, x_1, \cdots, x_{n-1} \) 所構成上述的方陣 \( V_n \), 其反矩陣的計算相當困難。幸運的是，有了 \( n \) 次單位根 (The principal nth root of unity) 和范德蒙矩陣 (Vandermonde matrix), 讓我們可以挑選適當的 \( x \) 座標以快速求得反矩陣的值。底下正式為他們做介紹。

\( n \) 次單位根 (The principal nth root of unity)

給定方程式 \( z^n = 1 \), 其中 \( n \) 為正整數，\( z \) 為複數。根據代數基本定理，該方程式有 \( n \) 個複數根，分別為 \( e^{\frac{2 \pi i \cdot 1}{n}}, e^{\frac{2 \pi i \cdot 2}{n}}, \cdots, e^{\frac{2 \pi i \cdot (n-1)}{n}}, e^{\frac{2 \pi i \cdot n}{n}}\), 其中最後一個數

$$ e^{\frac{2 \pi i \cdot n}{n}} = e^{2 \pi i} = \cos{2 \pi} + i \sin{2 \pi} = 1 $$

我們定義 \( \omega_n = e^{\frac{2 \pi i}{n}} \), 並稱 \( \omega_n \) 為 \( n \) 次單位根。例如：

\( \omega_2 \) 是 \( 2 \) 次單位根，且 \( \omega_2 = e^{\frac{2 \pi i}{2}} = e^{\pi i} = \cos{\pi} + i \sin{\pi} = -1 \)

\( \omega_4 \) 是 \( 4 \) 次單位根，且 \( \omega_4 = e^{\frac{2 \pi i}{4}} = e^{\frac{\pi}{2} i} = \cos{\frac{\pi}{2}} + i \sin{\frac{\pi}{2}} = i \).

回顧上方的方陣

$$ V_n = \left( \begin{matrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \end{matrix} \right) $$

當我們為 \( n-1 \) 次多項式挑選 \( x_0, x_1, \cdots, x_{n-1} \) 時，只要令 \( x_i = \omega^i_n \), 即可得到方陣

$$ V_n = \left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \cdots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{matrix} \right) $$

該方陣是一種接下來要介紹的范德蒙矩陣。

范德蒙矩陣 (Vandermonde matrix) 及其性質

范德蒙矩陣是一個每一列皆為等比數列的矩陣。下面是一個 \( m \times n \) 范德蒙矩陣的例子。注意到范德蒙矩陣不一定是方陣，每一列的公比也可以不全相同。

$$ \left( \begin{matrix} 1 & \alpha_1 & \cdots & \alpha_1^{n-1} \\ 1 & \alpha_2 & \cdots & \alpha_2^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & \alpha_m & \cdots & \alpha_m^{n-1} \end{matrix} \right)_{m \times n} $$

在 FFT 中，我們聚焦在以下這個特例 \( V_n \)：第 \( i \) 行和第 \( i \) 列的公比均為 \( \omega_n^{i-1} \) 且最左上角的元素為 \( 1 \) 的范德蒙方陣 \( V_n \) 上。注意這裡的行列均為 \( 1 \)-based.

$$ V_n = \left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \cdots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{matrix} \right) $$

由於反矩陣若存在必為一。經過驗證可以得到 \( V_n \) 的反矩陣如下

$$ V_n^{-1} = \frac{1}{n}\left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{-1} & \omega_n^{-2} & \cdots & \omega_n^{-(n-1)} \\ 1 & \omega_n^{-2} & \omega_n^{-4} & \cdots & \omega_n^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \cdots & \omega_n^{-(n-1)(n-1)} \end{matrix} \right) $$

因 \( \omega_n^n = 1\), 故 \( V_n^{-1} \) 可以改寫為

$$ V_n^{-1} = \frac{1}{n}\left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \\ 1 & \omega_n^{n-2} & \omega_n^{2(n-2)} & \cdots & \omega_n^{(n-1)(n-2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{1} & \omega_n^{2} & \cdots & \omega_n^{(n-1)\cdot 1} \end{matrix} \right) $$

[ 補充說明 ] 驗證反矩陣的過程中會用到 \( n \) 次單位根的四個性質，若讀者有興趣可以自行鑽研：

• 對於所有 \( n, k \geq 0 \), \( d > 0 \), \( \omega_{dn}^{dk} = \omega_{n}^k \).
• 對於所有正偶數 \( n \), \( \omega_{n}^{n/2} = \omega_{2} = -1 \).
• 對於所有正偶數 \( n \) 和非負整數 \( k \), 我們有 \( (\omega_{n}^{k+n/2})^2 = (\omega_n^k)^2 \).
• \( \omega_n^0 + \omega_n^1 + \cdots + \omega_n^{n-1} = 0 \).

有了 \( n \) 次單位根和范德蒙矩陣的協助，我們很輕鬆地解決了「求反矩陣」的困擾。不過即便得到一個快速算反矩陣的方法，仍需要 \( \Theta(n^2) \) 的時間將方陣中每個元素取倒數。

假設真的有方法能在 \( \Theta(1) \) 的時間內取得 \( V_n^{-1} \), 瓶頸則會出現在直接進行矩陣乘法上。無論是求向量 \( (A(\omega_n^0), A(\omega_n^1), A(\omega_n^2), \cdots, A(\omega_n^{n-1})) \) 或是 \( (a_0, a_1, \cdots, a_{n-1}) \) 都需要 \( \Theta(n^2) \) 的時間，並沒有做到任何優化。

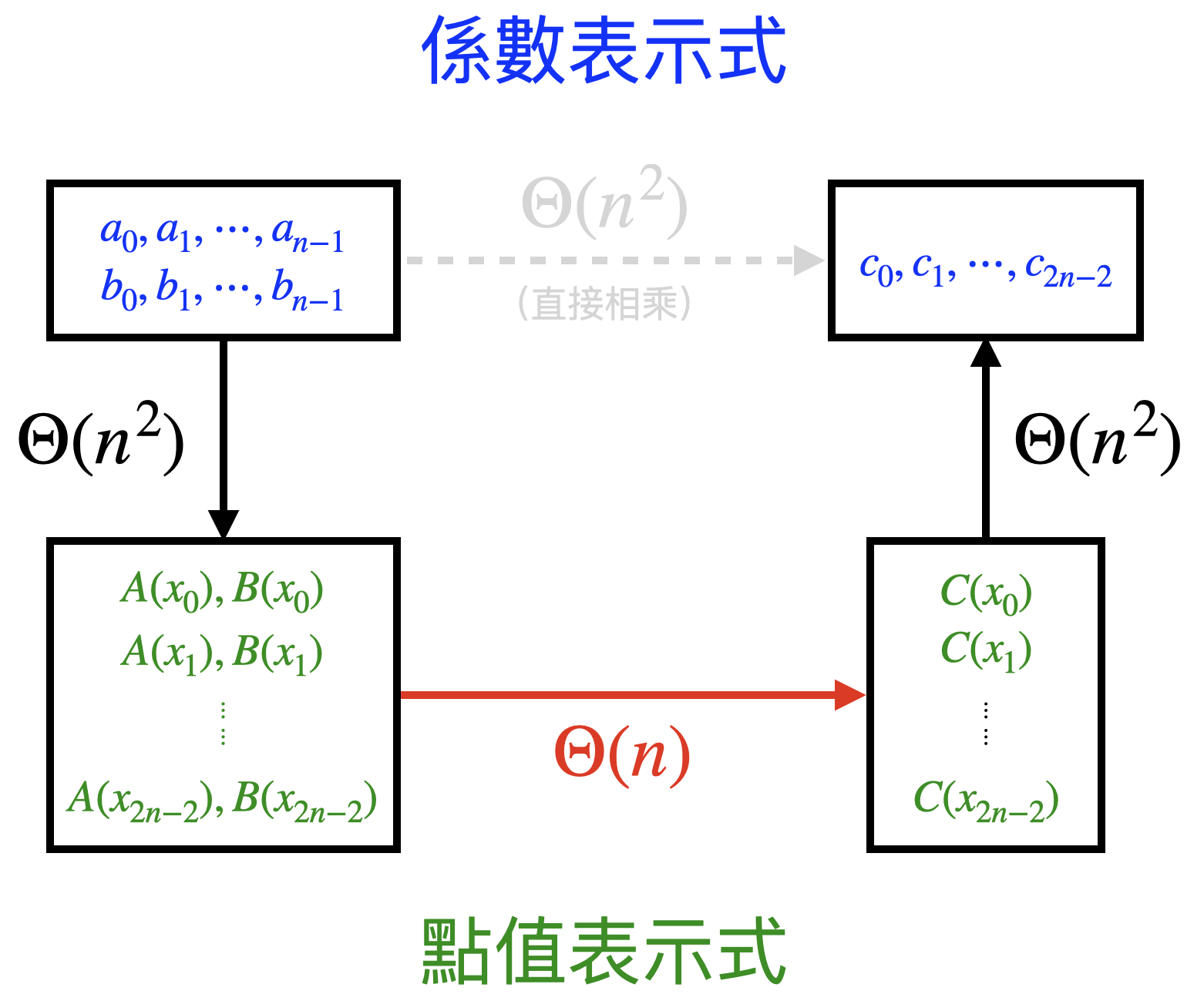
因此我們仍需要最後一個工具，也就是 FFT 的核心——分治法，幫助我們在 \( \Theta(n \log{n}) \) 的時間完成計算。

分治法計算

再次回到最初以係數表示法表示的 \( n-1 \) 次多項式 \( A(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_{n-1} x^{n-1} \). 我們將次方為奇數及次方為偶數的係數分別取出並形成兩個 \(\frac{n}{2}-1 \) 次多項式 \( A^{[0]}(x) \) 和 \( A^{[1]}(x) \), 其中

$$ A^{[0]}(x) = a_0 + a_2 \cdot x + a_4 \cdot x^2 + \cdots + a_{n-2} x^{\frac{n}{2}-1} $$ $$ A^{[1]}(x) = a_1 + a_3 \cdot x + a_5 \cdot x^2 + \cdots + a_{n-1} x^{\frac{n}{2}-1} $$

如此一來，原多項式 \( A(x) \) 可以表示為

$$ A(x) = A^{[0]}(x^2) + xA^{[1]}(x^2) $$

觀察發現計算 \( n \) 個 \( A(x) \) 值（也就是 \( A(\omega_n^0), A(\omega_n^1), A(\omega_n^2), \cdots, A(\omega_n^{n-1}) \)）所需的方陣是個 \( n \) 階方陣。對應到計算 \( A^{[0]}(x) \) 和 \( A^{[1]}(x) \), 只需求得 \( \frac{n}{2} \) 個值即可，所需的方陣是 \( \frac{n}{2} \) 階方陣。

具體而言，以 \( n = 8 \) 為例，若我們要計算 \( A(x) \) 在

$$ \omega_8^0, \omega_8^1, \omega_8^2, \cdots, \omega_8^7 $$

的值，則我們只需要計算 \( A^{[0]}(x) \) 和 \( A^{[1]}(x) \) 在

$$ \omega_8^0, \omega_8^2, \omega_8^4, \cdots, \omega_8^{14} $$

的值之後再合併即可。注意到

$$ \omega_8^0 = \omega_8^{8} = \omega_4^0 = 1 \\ \omega_8^2 = \omega_8^{10} = \omega_4^1 = i \\ \omega_8^4 = \omega_8^{12} = \omega_4^2 = -1 \\ \omega_8^6 = \omega_8^{14} = \omega_4^3 = -i $$

也就是我們只需要計算 \( A^{[0]}(x) \) 和 \( A^{[1]}(x) \) 在

$$ 1, i, -1, -i $$

一共 \( 4 \) 個值後做合併。所以計算 \( A(x) \) 所需的方陣為

$$ V_8 = \left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_8 & \omega_8^2 & \cdots & \omega_8^{7} \\ 1 & \omega_8^2 & \omega_8^4 & \cdots & \omega_8^{14} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_8^{7} & \omega_8^{14} & \cdots & \omega_8^{49} \end{matrix} \right) $$

而計算 \( A^{[0]}(x) \) 和 \( A^{[1]}(x) \) 所需的的方陣為

$$ V_4 = \left( \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & \omega_4 & \omega_4^2 & \omega_4^{3} \\ 1 & \omega_4^2 & \omega_4^4 & \omega_4^{6} \\ 1 & \omega_4^{3} & \omega_4^{6} & \omega_4^{9} \end{matrix} \right) $$

因此，欲計算 \( A(x) \), 我們只需要計算 \( A^{[0]}(x^2) \) 和 \( A^{[1]}(x^2) \) 後再合併即可。合併所需時間為 \( \Theta(n) \).

若以 \( T(n) \) 代表計算 \( A(x) \) 在 \( x = \omega_n^0, \omega_n^1, \cdots, \omega_n^{n-1} \) 所需的時間，我們可以列出關係式

$$ T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n) $$

得 \( T(n) = \Theta(n \log n) \). 事實上，這個運算就是 FFT.

到目前為止，我們只要再將點值表示式轉換成係數表示式就完成多項式的乘法了

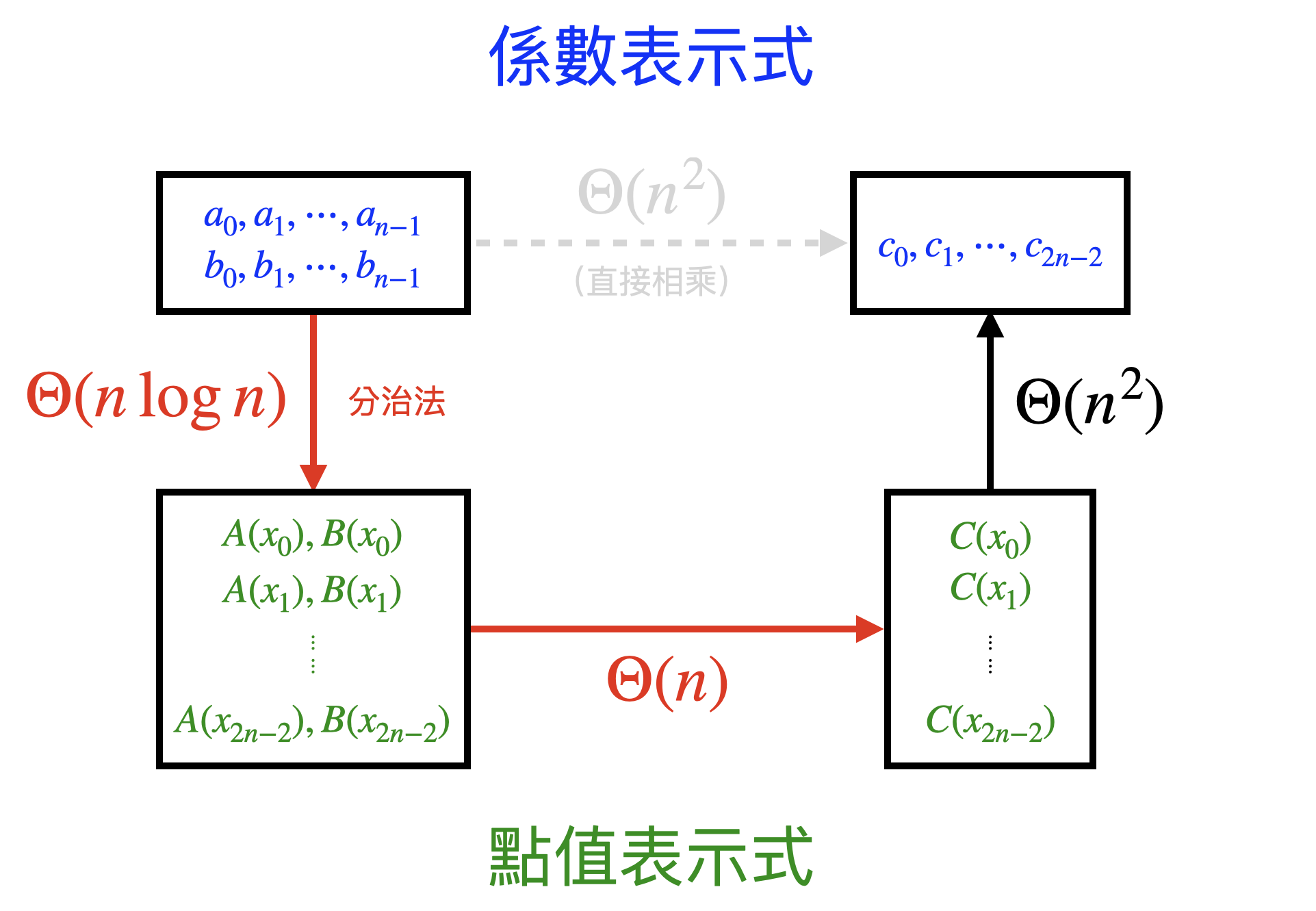
回顧剛才在 \( \Theta(n \log n) \) 的時間所做的矩陣運算，理論上是

$$ \left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \cdots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{matrix} \right) \left( \begin{matrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{matrix} \right) = \left( \begin{matrix} A(\omega_n^0) \\ A(\omega_n^1) \\ A(\omega_n^2) \\ \vdots \\ A(\omega_n^{n-1}) \end{matrix} \right) $$

實際上，我們在實作時所計算的矩陣是

$$ \left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_{2n} & \omega_{2n}^2 & \cdots & \omega_{2n}^{2n-1} \\ 1 & \omega_{2n}^2 & \omega_{2n}^4 & \cdots & \omega_{2n}^{2(2n-1)} \\ 1 & \omega_{2n}^3 & \omega_{2n}^6 & \cdots & \omega_{2n}^{3(2n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_{2n}^{2n-1} & \omega_{2n}^{2(2n-1)} & \cdots & \omega_{2n}^{(2n-1)(2n-1)} \end{matrix} \right) \left( \begin{matrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \\ 0 \\ \vdots \\ 0 \end{matrix} \right) = \left( \begin{matrix} A(\omega_{2n}^0) \\ A(\omega_{2n}^1) \\ \vdots \\ A(\omega_{2n}^{n-1}) \\ A(\omega_{2n}^{n}) \\ \vdots \\ A(\omega_{2n}^{2n-1}) \end{matrix} \right) $$

這是為了讓 \( C(x) \) 的點值表示式有足夠的點可以用。計算所需時間仍為 \( \Theta(n \log n) \).

上面是已知 \( (a_0, a_1, \cdots, a_{n-1}) \), 求 \( (A(\omega_{2n}^0), A(\omega_{2n}^1), \cdots, A(\omega_{2n}^{2n-1})) \)

而接下來是已知 \( (C(\omega_{2n}^0), C(\omega_{2n}^1), \cdots, C(\omega_{2n}^{2n-1})) \), 求 \( (c_0, c_1, \cdots, c_{2n-1}) \)

理論上已知 \( 2n-1 \) 個點就足夠，不過不影響答案和時間，甚至算 \( 2n \) 個點實作上會比 \( 2n-1 \) 個點簡單。

回顧運算式在等號兩邊要乘上的反矩陣為：

$$ \frac{1}{2n}\left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_{2n}^{-1} & \omega_{2n}^{-2} & \cdots & \omega_{2n}^{-(2n-1)} \\ 1 & \omega_{2n}^{-2} & \omega_{2n}^{-4} & \cdots & \omega_{2n}^{-2(2n-1)} \\ 1 & \omega_{2n}^{-3} & \omega_{2n}^{-6} & \cdots & \omega_{2n}^{-3(2n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_{2n}^{-(2n-1)} & \omega_{2n}^{-2(2n-1)} & \cdots & \omega_{2n}^{-(2n-1)(2n-1)} \end{matrix} \right) = \frac{1}{2n}\left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_{2n}^{2n-1} & \omega_{2n}^{2(2n-1)} & \cdots & \omega_{2n}^{(2n-1)(2n-1)} \\ 1 & \omega_{2n}^{2n-2} & \omega_{2n}^{2(2n-2)} & \cdots & \omega_{2n}^{(2n-1)(2n-2)} \\ 1 & \omega_{2n}^{2n-3} & \omega_{2n}^{2(2n-3)} & \cdots & \omega_{2n}^{(2n-1)(2n-3)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_{2n}^{1} & \omega_{2n}^{2} & \cdots & \omega_{2n}^{2n-1} \end{matrix} \right) $$

因此這裡要做的矩陣計算是：

$$ \frac{1}{2n}\left( \begin{matrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_{2n}^{2n-1} & \omega_{2n}^{2(2n-1)} & \cdots & \omega_{2n}^{(2n-1)(2n-1)} \\ 1 & \omega_{2n}^{2n-2} & \omega_{2n}^{2(2n-2)} & \cdots & \omega_{2n}^{(2n-1)(2n-2)} \\ 1 & \omega_{2n}^{2n-3} & \omega_{2n}^{2(2n-3)} & \cdots & \omega_{2n}^{(2n-1)(2n-3)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_{2n}^{1} & \omega_{2n}^{2} & \cdots & \omega_{2n}^{2n-1} \end{matrix} \right) \left( \begin{matrix} C(\omega_{2n}^0) \\ C(\omega_{2n}^1) \\ \vdots \\ C(\omega_{2n}^{n-1}) \\ C(\omega_{2n}^{n}) \\ \vdots \\ C(\omega_{2n}^{2n-1}) \end{matrix} \right) = \left( \begin{matrix} c_0 \\ c_1 \\ \vdots \\ c_{n-1} \\ c_{n} \\ \vdots \\ c_{2n-1} \end{matrix} \right) $$

由於這裡要計算的物理量和 FFT 所計算的不同且正好相反，所以這個計算也被稱作 Inverse FFT.

但本質上，兩個運算都是利用分治法，是相同的。具體而言可以把他理解為求多項式

$$ C(\omega_{2n}^0) + C(\omega_{2n}^1)x + \cdots + C(\omega_{2n}^{n-1})x^{n-1} + C(\omega_{2n}^{n})x^n + \cdots + C(\omega_{2n}^{2n-1})x^{2n-1} $$

在 \( x = \omega_{2n}^{0}, \omega_{2n}^{1}, \omega_{2n}^{2}, \cdots, \omega_{2n}^{2n-1} \) 的值再除以 \( 2n \). 因此所需時間為

$$ \Theta(n \log n) + \Theta(n) = \Theta(n \log n) $$

將上述所有步驟合併，即可得到完整的多項式乘法.

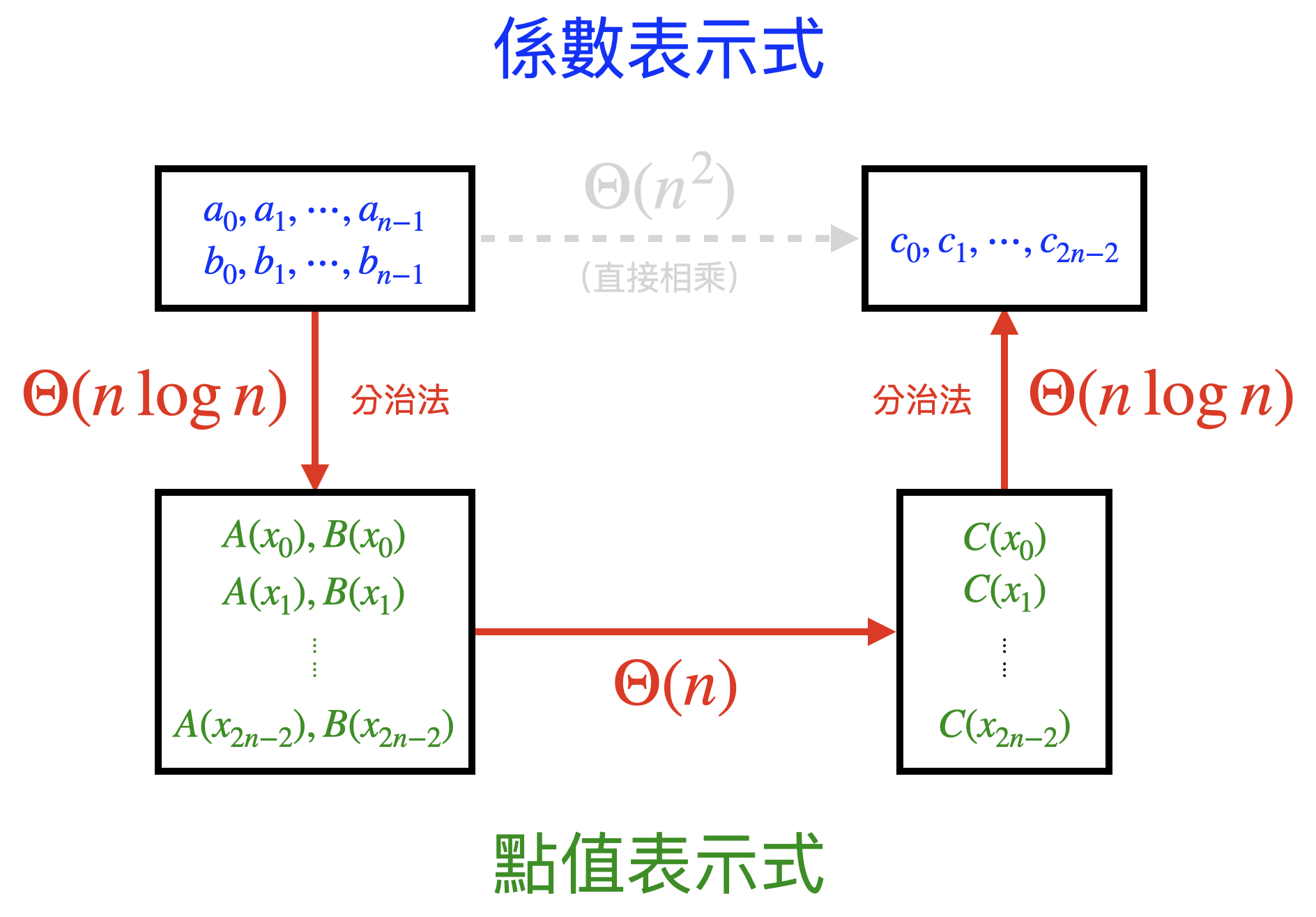
總結

欲計算兩個以係數表示式的多項式相乘，並以係數表示式呈現最後的結果，一共可分為以下三步驟。

• 將兩多項式 \( A(x), B(x) \) 的係數表示式利用 FFT 轉換成點值表示式，所需時間 \( \Theta(n \log n) \)
• 將對應的點值表示式兩兩相乘，得到 \( C(x) \) 的點值表示式，所需時間 \( \Theta(n) \)
• 將多項式 \( C(x) \) 的點值表示式利用 Inverse FFT 轉換成係數表示式，所需時間 \( \Theta(n \log n) \)

故總時間為 $$ \Theta(n \log n) + \Theta(n) + \Theta(n \log n) = \Theta(n \log n) $$

模板與習題

模板

\( \omega_n \) 涉及三角函數的計算。為了確保浮點數的精確度，我們使用變數型態 double 宣告浮點數。

進行乘法時，我們使用 long long 作為陣列中每個元素的變數型態以為避免長整數溢位。

// The function gets passed a vector of coefficients.
// It will compute the FFT or inverse FFT,
// and store the result again in this vector.
// invert = 1 -> inverse FFT
// invert = 0 -> FFT
using cd = complex<double>;
const double PI = acos(-1);

void fft(vector<cd> & a, bool invert) {
    int n = a.size();
    if (n == 1)
        return;

    vector<cd> a0(n / 2), a1(n / 2);
    for (int i = 0; 2 * i < n; i++) {
        a0[i] = a[2*i];
        a1[i] = a[2*i+1];
    }
    fft(a0, invert);
    fft(a1, invert);

    double ang = 2 * PI / n * (invert ? -1 : 1);
    cd w(1), wn(cos(ang), sin(ang));
    for (int i = 0; 2 * i < n; i++) {
        a[i] = a0[i] + w * a1[i];
        a[i + n/2] = a0[i] - w * a1[i];
        if (invert) {
            a[i] /= 2;
            a[i + n/2] /= 2;
        }
        w *= wn;
    }
}

// multiplying two polynomials
vector<long long> multiply(vector<long long> const& a, vector<long long> const& b) {
    vector<cd> fa(a.begin(), a.end()), fb(b.begin(), b.end());
    long long n = 1;
    while (n < a.size() + b.size()) 
        n <<= 1;
    fa.resize(n);
    fb.resize(n);

    fft(fa, false);
    fft(fb, false);
    for (long long i = 0; i < n; i++)
        fa[i] *= fb[i];
    fft(fa, true);

    vector<long long> result(n);
    for (long long i = 0; i < n; i++)
        result[i] = round(fa[i].real());
    return result;
}

模板題

SPOJ - Polynomial Multiplication

給定兩個 \( n \) 次多項式的係數，輸出兩個多項式相乘的多項式係數。

#include <iostream>
#include <cmath>
#include <complex>
#include <vector>

using namespace std;
using cd = complex<double>;
const double PI = acos(-1);

void fft(vector<cd> & a, bool invert) {
    int n = a.size();
    if (n == 1)
        return;

    vector<cd> a0(n / 2), a1(n / 2);
    for (int i = 0; 2 * i < n; i++) {
        a0[i] = a[2*i];
        a1[i] = a[2*i+1];
    }
    fft(a0, invert);
    fft(a1, invert);

    double ang = 2 * PI / n * (invert ? -1 : 1);
    cd w(1), wn(cos(ang), sin(ang));
    for (int i = 0; 2 * i < n; i++) {
        a[i] = a0[i] + w * a1[i];
        a[i + n/2] = a0[i] - w * a1[i];
        if (invert) {
            a[i] /= 2;
            a[i + n/2] /= 2;
        }
        w *= wn;
    }
}

vector<long long> multiply(vector<long long> const& a, vector<long long> const& b) {
    vector<cd> fa(a.begin(), a.end()), fb(b.begin(), b.end());
    long long n = 1;
    while (n < a.size() + b.size()) 
        n <<= 1;
    fa.resize(n);
    fb.resize(n);

    fft(fa, false);
    fft(fb, false);
    for (long long i = 0; i < n; i++)
        fa[i] *= fb[i];
    fft(fa, true);

    vector<long long> result(n);
    for (long long i = 0; i < n; i++)
        result[i] = round(fa[i].real());
    return result;
}

void solve() {
    long long n;
    cin >> n;
    vector<long long> a(n+1), b(n+1);
    for (long long i = 0; i <= n; ++i) cin >> a[i];
    for (long long i = 0; i <= n; ++i) cin >> b[i];
    vector<long long> result = multiply(a, b);
    for (long long i = 0; i <= (n << 1); ++i) cout << result[i] << " ";   cout << "\n";
    return;
}

int main() {
    long long T;
    cin >> T;
    while(T--)
        solve();
    return 0;
}

例題

SPOJ - Maximum Self-Matching

給定一個只包含 'a' , 'b' 和 'c' 的字串 s .

定義 \( m_{s}(i) \) 為字串 s 向右移動 \( i \) 個字元後與自己匹配的字元個數，其中 \( 1 \leq i < \lvert \) s \( \rvert \).

求最大的 \( m_{s}(i) \) 值。

設該值為 \( M \), 再求所有符合 \( m_{s}(i) = M \) 的 \( i \) 值。

#include <iostream>
#include <cmath>
#include <complex>
#include <vector>

using namespace std;
using cd = complex<double>;
const double PI = acos(-1);

string s;
int slen;

void fft(vector<cd> & a, bool invert) {
    int n = a.size();
    if (n == 1)
        return;

    vector<cd> a0(n / 2), a1(n / 2);
    for (int i = 0; 2 * i < n; i++) {
        a0[i] = a[2*i];
        a1[i] = a[2*i+1];
    }
    fft(a0, invert);
    fft(a1, invert);

    double ang = 2 * PI / n * (invert ? -1 : 1);
    cd w(1), wn(cos(ang), sin(ang));
    for (int i = 0; 2 * i < n; i++) {
        a[i] = a0[i] + w * a1[i];
        a[i + n/2] = a0[i] - w * a1[i];
        if (invert) {
            a[i] /= 2;
            a[i + n/2] /= 2;
        }
        w *= wn;
    }
}

vector<long long> multiply(vector<long long> const& a, vector<long long> const& b) {
    vector<cd> fa(a.begin(), a.end()), fb(b.begin(), b.end());
    long long n = 1;
    while (n < a.size() + b.size()) 
        n <<= 1;
    fa.resize(n);
    fb.resize(n);

    fft(fa, false);
    fft(fb, false);
    for (long long i = 0; i < n; i++)
        fa[i] *= fb[i];
    fft(fa, true);

    vector<long long> result(n);
    for (long long i = 0; i < n; i++)
        result[i] = round(fa[i].real());
    return result;
}

int main() {
    cin >> s;
    slen = s.length();
    vector<long long> total(slen, 0), p(slen), r(slen), tmp;
    
    for (int i = 0; i < slen; ++i)  p[i] = r[slen - 1 - i] = (s[i] == 'a' ? 1LL : 0LL);
    tmp = multiply(p, r);
    for (int i = 0; i < slen; ++i)    total[i] += tmp[i];

    for (int i = 0; i < slen; ++i)  p[i] = r[slen - 1 - i] = (s[i] == 'b' ? 1LL : 0LL);
    tmp = multiply(p, r);
    for (int i = 0; i < slen; ++i)    total[i] += tmp[i];

    for (int i = 0; i < slen; ++i)  p[i] = r[slen - 1 - i] = (s[i] == 'c' ? 1LL : 0LL);
    tmp = multiply(p, r);
    for (int i = 0; i < slen; ++i)    total[i] += tmp[i];

    int ans = -1;
    for (int i = 0; i < slen-1; ++i)
        if (total[i] > ans)
            ans = total[i];
    cout << ans << "\n";
    for (int i = slen - 1; i >= 0; --i)
        if (total[i] == ans)
            cout << slen - 1 - i << " ";
    if (ans == 0)   cout << slen << " ";
    cout << "\n";
    return 0;
}

練習題

SPOJ - Ada and Nucleobase

給定兩個 DNA 序列 s 和 r , 其中 r 的長度比 s 短。

輸出 r 在 s 所有長度為 \( \lvert \) r \( \rvert \) 的連續子字串中，hamming distance 的最小值。

Codeforces 958 F3 - Lightsabers (hard)

給定 \( n \) 個介於 \( 1 \) 到 \( m \) 的正整數，求從 \( n \) 個數中任取 \( k \) 個數有幾種不同的取法。

Codeforces 954 I - Yet Another String Matching Problem

假設有兩個長度相等的字串 s 和 t . 我們可以不限次數地做以下操作：

任選兩個不同的字元 \( c_1, c_2 \), 並將 s 和 t 中所有的 \( c_1 \) 換成 \( c_2 \).

定義兩字串 s 和 t 的距離為：使用最少的操作數將 s 和 t 變成一樣的字串。

今天給定兩字串 S , T , 兩字串僅包含字元 'a' , 'b' , 'c' , 'd' , 'e' , 'f' .

我們要計算每個 S 中長度為 | T | 的字串與 T 的距離。

Reference

• Introduction to Algorithms Fourth Edition p. 877 ~ p. 893
• CP Algorithm, Fast Fourier transform
• SPOJ - Polynomial Multiplication
• SPOJ - Maximum Self-Matching
• SPOJ - Ada and Nucleobase
• Codeforces 958 F3 - Lightsabers (hard)
• Codeforces 954 I - Yet Another String Matching Problem